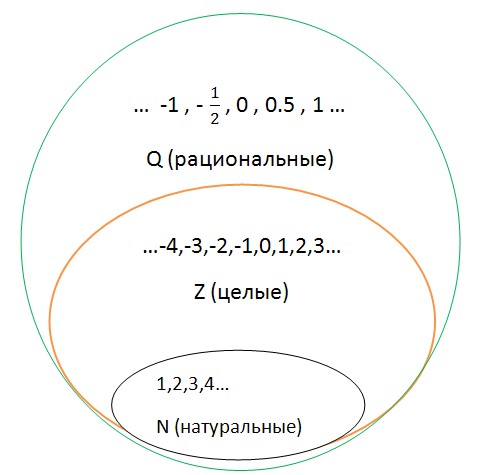
Как известно, множество действительных чисел состоит из рациональных и иррациональных, и притом каждое действительное число можно представить в виде бесконечной десятичной дроби. Правда, десятичная запись рациональных и иррациональных чисел отличается. Например, 1:3 (одна третья) мы можем представить как 0,0333… = 0,(3), а (корень из двух) √2= 1,4142… и, сколько бы Вы не писали дальше, в иррациональных числах период не появится.
Я вам хочу рассказать о том, как, наоборот, из периодических дробей делать обыкновенные, из 0,(3) делать 1:3 (одну третью) и т.д.. Для этого давайте возьмем число 0,(41), которое равно а. Тогда 100а = 41,(41). Вычтем из первое равенство из второго:
100а – а = 41,(41) – 0,(41), 99а = 41. Значит а = 41:99 (сорок одна девяносто девятая).
Несколько сложнее получается, когда дробь смешанная и период начинается не сразу. Но и для такого случая есть выход. Рассмотрим а = 0,3(18). Значит
10а = 3,(18) , 1000а = 318,(18). Потом мы опять отнимаем от второго равенства первое и получаем 990а = 315. а = 315:990 = 7:22 (семь двадцать вторых).
Вот и все.
