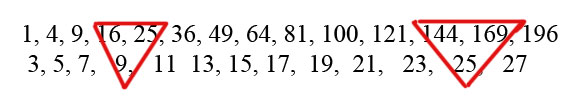
Ми добре знаємо сторони Єгипетського трикутника 3, 4, 5.
А чи є ще такі трійки чисел? Чи можна, взявши одне довільне число, вказати інші два? Ці питання цікавили ще мудреців Стародавнього Вавілону. Вони знайшли відповідь на них. Знав це й Піфагор. Один з шляхів вирішення рівняння x2+y2=z2 в цілих числах виявився доволі простим. Запишемо підряд квадрати натуральних чисел (“квадратні числа”, як їх називали в стародавньому світі), відділивши їх одне від одного комами. Під комжною комою запишемо різницю між послідовними квадратами.
А тепер увага! В нижньому рядку є квадратні числа! Перше з них 9=32 х, над ним 16=4 і 25=5, знайома нам трійка трикутника 3, 4, 5.
Наступне квадратне число у нижньому ряду 25, йому відповідають 144 і 169, звідси знаходимо другу трійку 5, 12, 13, яку ми часто зустрічаємо при розв‘язуванні задач. Якщо продовжити ряд квадратних чисел і порахувати відповідні різниці, то в другому рядку знаходимо 49=72, цьому числу відповідають в рядку квадратів 576=242 і 625=252. І дійсно 72+242=252. Це вже третя трійка, вона була відома ще в Стародавньому Єгипті.
Ці формули-правила були відомі вже дві з половиною тисячі років тому. А використовувати цей спосіб знаходження піфагорових трійок є дуже простим і цікавим.
