У дев’ятому класі ми вивчили подібність трикутників, вирішили багато задач з цієї теми. Але рівень шкільних задач зводиться до першої ознаки подібності трикутників. Тож я пропоную вам навчитися вирішувати більш складні задачі за допомогою узагальненої теореми подібності. Звучить вона так: якщо два 3-кутники подібні, то відношення Їх відповідних сторін дорівнює відношенню лінійних вимірів або суми лінійних вимірів:h, l, m, P, r, R(висот, бісектрис, медіан, периметрів, радіусів вписаного та описаного кіл)
Для приклада розв’яжемо таку задачу:
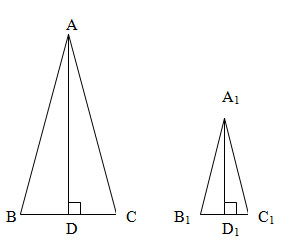
Сторона і основа рівнобедреного трикутника дорівнюють 25 і 30 см відповідно. Знайдіть основу і бічну сторону подібного йому трикутника, висота якого, опущена на основу, дорівнює 4 см.
Розвязання
1.Для того, щоб знайти A1 B1 і B1C1, з ∆ABC знайдемо висоту АD.
BD= BC/2= 15 см
АD2=AB2-BD2 = 252-152=202
АD=20 см
2.
(за узагальненою теоремою подібності)
A1 B1 = 5 см
B1C1= 6 см
Відповідь: 5 см і 6 см
Таким чином, ми використали відношення сторін та висот, для розв’язання цієї задачі.
Узагальнена теорема подібності дуже корисна для розв’язування складних задач, навіть олімпіадного рівня.